成都網站建設_數學與網頁設計之間的密切關系
2022-12-18 分類: 網站建設
數學無處不在,即使你不喜歡它。 你可以在建筑中找到數學比例和常數,也可以在樂器中找到它們。 我們常玩的游戲里也有,所以就不要為數學在網頁設計中扮演了重要角色而感到驚訝咯。 但是它是什么呢? 我們該如何使用這些比例,常數和理論來是的我們的網頁設計更加美觀?
數學無處不在
沃爾特·迪斯尼曾經在Mathmagicland拍了一部關于唐老鴨的電影。 在YouTube上提供的這個視頻中,他們會向兒童介紹數學及其用途。 它表明使用數學比例來定義儀器上的音符,并且可以在古代和現代建筑中找到數學矩形。 此外,我們可以在一些文藝復興時期的藝術中找到這個完全相同的矩形,例如著名的蒙拉麗莎的微笑。

簡單的小課程:你可以使用一些基本的數學原理來使得自己的設計更為美觀。
小故事
在古希臘,有一群數學家稱自己是畢達哥拉斯人。 畢達哥拉斯人以五角星為標志。 他們選擇這種形狀,因為它的數學好:五角星的線性形狀中包含著黃金比例! 此外蒙娜麗莎的微笑里面也隱藏著黃金矩形。
兔子養殖
在十二世紀和十三世紀,有一位才華橫溢的意大利數學家。 他的名字是斐波那契。他觀察到兔子的自然繁殖。 在他這個理想的世界里,兔子不會死亡,每只兔子都竭力繁殖, 他發現這個周期里有一個特殊的數字序列。 這個序列后來被稱為斐波納契數字。

關于這個序列的特別之處在于,如果您按序列中的數字劃分所選數字,則每次都會(大約)獲得相同的數字。 這個數字約為1.618,更好地稱為Phi。按順序進一步,分割結果越接近Phi。 斐波那契還發現,這個序列不僅存在于兔子的育種中, 而且在自然界的其他物質中也存在著,例如種子在向日葵中的排列。
黃金比例
正如你已知道的,Phi是非常常見的設計常數。 這是因為1比1.618被稱為黃金比例,或者說是黃金分割。如果按照這個比例繪制一個矩形,就會得到一個黃金矩形。
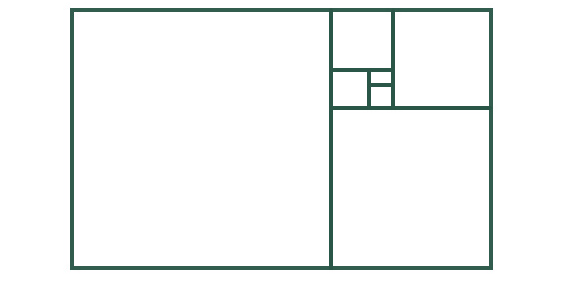
這里顯示的黃金矩形展示了如何將其自身無限好分割。
黃金比例和黃金矩形用于許多設計中,在文藝復興時期,許多藝術家按這個比例和矩形來繪制他們的作品。 在古希臘,建筑師在建筑物的設計中使用黃金矩形, 帕特農神廟就是個很好的例子。 即使在現代建筑中,黃金矩形也有很強的存在感。
但是,這個比例為什么這么特別呢? 因為Phi,是個自然數學常數,我們會自動的對這個比例的東西感到滿意 因為我們很熟悉這個比例,觸發一種韻感。 因此使用黃金比例可以保證你設計中的元素構成平衡。
網頁設計中黃金比例的例子
在我們甚至開始考慮將這個比例應用于我們的設計之前,我們首先要看一下使用這個比例的幾個例子。
首先是這個網站,它的設計有多個比例構成。 在下面的圖片里你將看到網站的界面。 我用了兩種顏色來標記不同的構成, 主要列的寬度比恰好是1.618, 像素點的計算證明了這一點。
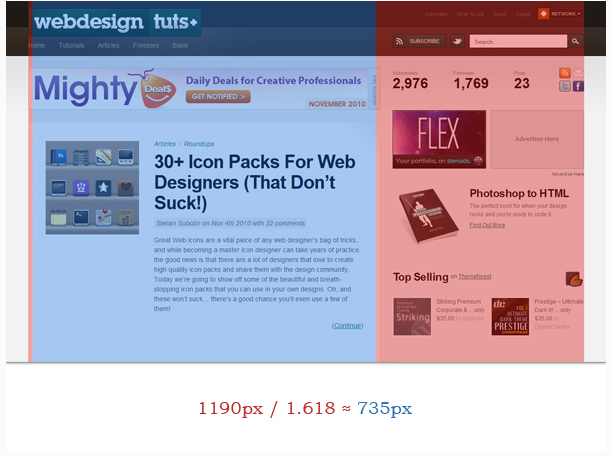
但是這個網站不僅在總寬度上使用黃金比例,還適用于網站上一些較小的部分。
讓我們快速瀏覽主列,然后看看內容。 如下所示,文本元素大概是此元素中藥讀取內容的1.618倍。
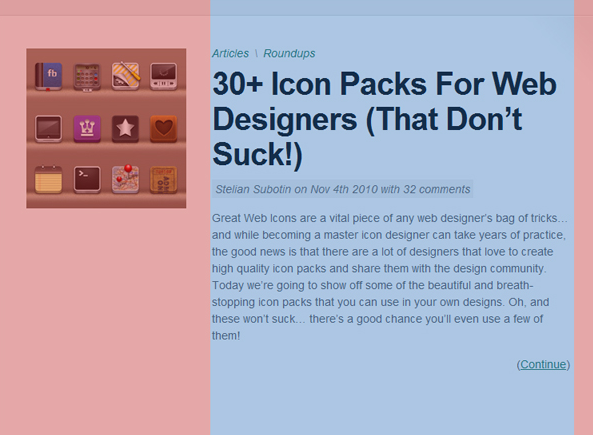
另一個很好的例子是著名的Smashing Magazine博客。 其主列的總寬度僅為700像素。 當您將此數字除以1.618時,結果是大約435:側邊欄的寬度。
如何將這個比例應用于你的下一個設計中
繪畫的畫布和建筑物的寬度都具有固定的寬度 ,但是我們的的顯示器的大小不同。因此,尤其是在網站設計中,在計算黃金比例時應考慮一個額外的變量。
但是有一個簡單的辦法來解決這個問題, 你根據比例計算寬度的時候,只需要計算包含元素。 在我們的第一個和最后一個例子中, 這是一個網站的完整寬度,在第二個例子中,只是較小部分的寬度:它們的主列。
無論如何,當你確定包含元素的寬度時,你應該將此值除以Phi, 然后獲得主要元素的寬度。 然后從元素寬度中減去主要元素的結果,這將給出較小部分的寬度。
如果你懶得記Phi或者懶得用計算器,我建議用Phiculator, 這個小程序只需要填寫總寬就能自動計算寬度。 它能整數計算,不必擔心十進制數字計算會出問題。
三分法則
另一個著名的數學法則是三分法則。 這個規則將幫助你將畫面分為九個相等的部分來制作平衡的組合。 這個規則有點類似于黃金比例,因為0.618和0.67約等于三分之二。
攝影
在攝影中,經常使用三分法則來構圖拍攝,因為它是個很直觀的指導,容易拍出好的照片。 這就是為什么你會在單反上看到網格線的原因。 有些微單也有這個功能,在攝影的時候加入網格點。
它是如何指導工作的?
使用三分法則, 你可以將畫布分為九個相等的矩形,平行線和四個交點, 你可以使用平行線和交點創造出有趣的組合。
顯然,組合的關鍵在正確定位元素, 使用三分法則的時候,你可以做兩件事。
第一個是用于劃分畫布的線條, 攝影中,長而直的形狀通常與這些線對齊。 在設計中,具有相同形狀的東西也可以與這些線對齊。
第二件事是,你需要在交點上放置一個或兩個對象, 太多會影響構圖。
這是我在攝影網站Flickr上發現的一個很好的例子。 如下圖所示攝影師將排列的建筑物與頂線對齊,而在右上角的交叉點,您會發現一個房子,因為它的顏色最突出。 因為它本身就是一個焦點,它與交點相一致,增加了良好的組合和均衡的感覺。

Flickr上發現的照片
我們已經看到了三分法則適用于攝影中,但是如何將其用于網站設計,我們可以找到例子嗎?
網頁設計三份法則
網站設計中一個很好的例子就是這個。 我準備了一個你將看到的圖片。 側邊欄和右邊的垂直線非常接近, 在左側,你可以看到文章位于交點上。
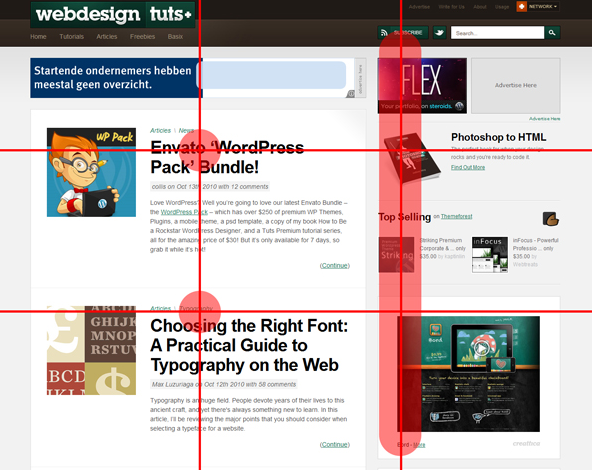
你在上面看到的兩個對齊垂直線在這個網站的布局中創造出一種和諧的感覺。
將三分法則應用于你的下一個設計
三分法則究竟能適用于你的網站的設計嗎? 另外,我們的“畫布”的寬度變化可能會帶來一些麻煩。 當我們使用與黃金比例相同的技術時,我們會很好。
要應用這個法則,你必須把你的總寬分為三份, 然后畫出指導線,然后重復。
但是,第二部分可能有點麻煩,我們畫布的高度是可變的, 將變量除以三將給我們帶來麻煩。 我喜歡用寬屏比例來計算分數的高度,或者只是使用包含元素的高度。 將包含元素的寬度除以16再乘以9,就得到了高度, 然后除以3并繪制指導線。
當你設置了指導線,你可以根據這些指導線來定位你的元素。 將你的元素與線對齊,將一些亮點放置在交點上。
網格系統
你可能認為網格系統并不是數學的,但是它們是的。 你將畫布分為不同的列和溝槽,這個劃分由黃金法則和三分法則計算。
很多人認為網格系統會限制設計師的創造力,因為得根據系統來繪圖。 我不認可這個觀點,因為網格系統實際上提高了創造力, 你會看到很多的構成,會想辦法去解決它們,而如果沒有網格系統,你將永遠不會考慮它們。
網格系統的工作原理是引導你進行大小、定位、調整網站設計。 它們可以幫助你組織規范的界面,消除混淆的版塊。 最重要的是它們便于使用。
使用網格系統的另一個好處是規則就是用來打破的,不是嗎? 如果你打斷你的網格的一部分, 這并不錯誤! 可以為界面上的特定元素制作出特別的點,因為它與其他元素有著鮮明的對比。 這可以幫助你實現某些目的,比如標語。
如何制作一個好的網格
沒有任何一個網格是適用于任何設計的,因為網格圍繞內容來制作。 我將演示如何在960像素寬的環境中構建6列網格的簡單過程。
首先,我們將我們的總畫布寬度除以6,所以我們有每列的總寬度。 這個劃分的結果是160像素,如下圖所示。
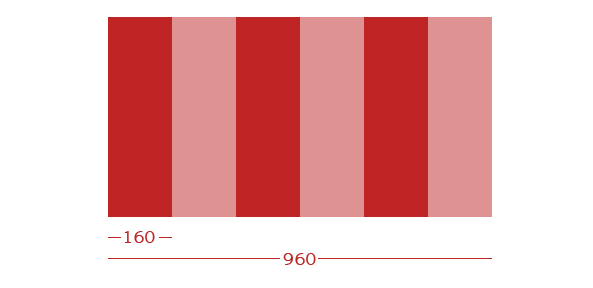
其次,我們將創建一個圖像的一列,我們稍后將復制。 樣一來,以后就更容易創建完整的網格,因為我們不必為每一列重復這一步。
我們將決定我們的間隔的大小,我認為20像素就足夠了。 這個間隔應該被添加到列的兩邊,所以我們必須把它除以2。 這個間隔應該被添加到列的兩邊,所以我們必須把它除以2。 如下圖所示,我們在每邊添加了一個10像素的間隔。

然后我們將再次復制這個圖像,直到再次達到960個像素,這個時候我們已經創建了一個基本的網格系統了。
我很懶!
別擔心,哪怕你懶, 互聯網上也有很多的免費網格系統可以使用。 我最喜歡的是960gs網格系統,它具有一個CSS框架和PSD源文件。

總結
我希望我向你展示了數學是可以使設計變得更加美好,我已經教給你在下一個設計中使用得很多技巧。 不過需要注意的是,設計中還需要考慮到很多問題,并不是僅僅使用這些技巧就能創造出良好的設計,但是它們確實可以幫助到你進行創造。
創新互聯專業從事成都網站建設,成都網站設計,成都網站制作
網站題目:成都網站建設_數學與網頁設計之間的密切關系
網頁鏈接:http://newbst.com/news19/223669.html
網站建設、網絡推廣公司-創新互聯,是專注品牌與效果的網站制作,網絡營銷seo公司;服務項目有網站建設等
聲明:本網站發布的內容(圖片、視頻和文字)以用戶投稿、用戶轉載內容為主,如果涉及侵權請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網站立場,如需處理請聯系客服。電話:028-86922220;郵箱:631063699@qq.com。內容未經允許不得轉載,或轉載時需注明來源: 創新互聯
猜你還喜歡下面的內容
- 網站建設以前必須做些哪些 2022-12-18
- 淺談一個網站建設的三步曲 2022-12-18
- 企業跟公司為什么需要要做網站建設 2022-12-18
- 廣州婚慶網站建設要如何設計? 2022-12-18
- 選擇網站建設公司主要考察哪些方面? 2022-12-17
- 廣州電商網站建設的五大原則有哪些? 2022-12-17
- 在成都網站建設行業里響應式設計為什么如此重要? 2022-12-17
- 淺析個人網站建設需要注重的建設問題 2022-12-17
- 成都創新互聯:網站建設常用的工具有哪些? 2022-12-17
- SEO對于網站建設有哪些要求 2022-12-17

- 如何尋找適合的網站建設公司? 2022-12-18
- 高端營銷網站建設方案的三個主要好處 2022-12-17
- 成都專業網站建設公司做網站時需要什么材料 2022-12-17
- 服裝網站建設整套設計流程講解 2022-12-17
- 幫助你如何正確挑選網站建設公司! 2022-12-17
- 佛山網站建設流程是怎樣的? 2022-12-17
- 網站建設你不可不知的五大知識 2022-12-17
- 重慶網站建設詳解ico圖標制作過程 2022-12-17
- 洽談網站建設業務前需要做的準備工作 2022-12-17